Octave 머신러닝

출력

---

fprintf('octave')

 

identity matrix 

---

5x5 정사각행렬에서 주대각선의 원소가 모두 1이고, 다른 원소는 모두 0인 행렬 을 만든다

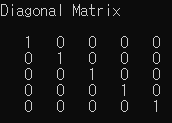
I = eye(5);

 

데이터 로드

---

octave 에서는 주석을 쓸때 % 를 씁니다

data = load('data1.txt'); 

X = data(:, 1); % 전체 데이터에서 1번째 행
y = data(:, 2); % 전체 데이터에서 2번째 행
m = length(y); % 트레이닝 세트의 개수 

 

플롯(plot) 만들기

---

plot(x, y, 'rx', 'MarkerSize', 10); % 데이터로 플롯(plot)을 만든다
ylabel('y'); % y 축 레이블
xlabel('x'); % x 축 레이블

 

 

 

선형회귀 Linear Regression with one variable

---

경사하강법 (Gradient Descent)

X = [ones(m, 1), data(:,1)]; % y 길이만큼의 1로된 열을 만들어 추가한다
theta = zeros(2, 1); 2행 1열 0 행렬 생성(theta = [0 ; 0])
iterations = 1000; 
alpha = 0.01; % 학습률(learning rate)

theta 값이 0 이면 h(x) = 0+0x 가된다.

 

비용함수 (Cost Function)

비용함수 Cost Function

h_o(x) 계산

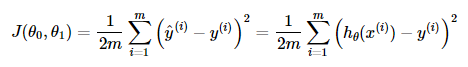
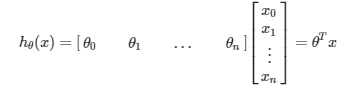
% computeCost
function J = computeCost(X, y, theta)

% 비용함수 J를 0 으로 초기화
m = length(y)
J = 0;

J = (1/(2 * m)) * (sum(((X * theta) - y) .^ 2));
end

 

gradient descent 실행

% GradientDescent
function [theta, J_history] = gradientDescent(X, y, theta, alpha, num_iters)

% m과 J_history를 초기화
m = length(y);
J_history = zeros(num_iters, 1);

for iter = 1:num_iters
    theta = theta - alpha*(1/m) * (X' * ((X * theta) - y));
    J_history(iter) = computeCost(X, y, theta); % iteration 마다 cost J 를 저장  

end

end

 

% 비용계산
J = computeCost(X, y, theta);
% theta = [0 ; 0] 사용
% 약 32.07이 나온다


J = computeCost(X, y, [-1 ; 2]);
% theta = [-1 ; 2] 사용
% 약 54.24

%경사하강 실행
theta = gradientDescent(X, y, theta, alpha, iterations);

% 쎄타값 출력
% -3.6303, 1.1664
fprintf('%f\n', theta);